Time y Space Complexity: métricas para construir algoritmos escalables

Time y Space Complexity: métricas para construir algoritmos escalables

Francisco

-
Sígueme en:
linkedin icongithub icon
Publicado el: Dec 28, 2025
Compartir:

La mayoría de las veces no pensamos mucho en el rendimiento de nuestros algoritmos y códigos, aún menos en esta era de la IA, donde una parte del código está siendo construida por agentes más que por humanos. No obstante, cuando hay miles de datos y el problema no es trivial de resolver, es sumamente relevante preguntarse si la solución es lo suficientemente robusta y eficiente, y si lo generado por los agentes de IA es realmente lo más óptimo o simplemente una solución local.

La complejidad algorítmica es un tema que ha sido ampliamente estudiado desde hace década atrás y cualquier algoritmo o solución eficiente debería considerar, al menos, las siguientes dimensiones:

1. Time complexity: ¿Qué tan rápido es el algoritmo?
2. Space complexity: ¿Cuánta memoria computacional se requiere?

Time complexity: Menos es más.

El time complexity no está relacionado con el nivel de hardware de tu computadora, sino que mide la cantidad de operaciones realizadas por un algoritmo hasta completar su ejecución, y se expresa principalmente en función del tamaño de la entrada.

Cuando la entrada es pequeña (inputs), generalmente no es necesario preocuparse demasiado por el time complexity. Sin embargo, a medida que el tamaño de la entrada crece, el tiempo de ejecución puede aumentar de forma exponencial. A esto se le conoce como el comportamiento asintótico de los algoritmos.

Ejemplo

Supongamos que el tiempo de un algoritmo está dado por:

f(n)=n*n+3n

Dado el n como el numero de entrada.

Cuando n es pequeño, ambos términos importan en similar magnitud.
Pero cuando n crece mucho, el término 3n se vuelve poco relevante comparado con n*n. (ya que crece a menor escala).

Por eso decimos que, para valores grandes de n, el comportamiento de esta función es básicamente:

f(n)≈n*n

O, dicho de otra forma, el algoritmo tiene complejidad O(n*n).

Idea concreta:
Pensemos por un momento en un ejemplo un poco más concreto. Imaginemos que eres un profesor que debe evaluar las tareas de todos sus estudiantes. Tus labores son:

  1. Comparar la tarea de cada estudiante con la de los demás para detectar si existen copias.
  2. Colocar la nota correspondiente a cada prueba.

Este trabajo tiene dos partes: una con complejidad n y otra con complejidad n · n. Si esto fuera una función en Python, se podría representar de la siguiente manera:

1def review_tests(d: dict):
2    keys = list(d.keys())
3    values = [d[k] for k in keys]
4

5

6    dup_flags = np.zeros(len(keys), dtype=bool)
7    for i in range(len(values)):
8        for j in range(len(values)):
9            if i != j and values[i] == values[j]:
10                dup_flags[i] = True
11                break
12

13    ground_truth = "I think it's 7"
14    for k in d:
15        d[k] = 5 if d[k] == ground_truth else 0
16

17    return {
18        'array': dup_flags,
19        'note': d
20    }

Este algoritmo tiene dos tipos de operaciones: comparaciones y asignaciones de nota. Si necesitamos revisar cada una de las pruebas y compararlas entre sí, el número de comparaciones crece aproximadamente como n*n. Luego, asignar la nota a cada alumno agrega un costo adicional de n.

Por lo tanto, el tiempo total es n*n+n, y su complejidad asintótica es O(n²).

Con 10 alumnos esto es rápido, pero con 100 o 1000 alumnos el número de operaciones aumenta mucho (por ejemplo, con 1000 alumnos es del orden de un millón). En escenarios reales, como millones de transacciones, un enfoque cuadrático puede volverse impracticable y conviene buscar alternativas más eficientes.

La teoría: Relación entre la complejidad, su numero de operaciones y tamaño del input.

Se ha estudiado la relación entre el tamaño de las operaciones, el número de inputs y la complejidad algorítmica de diversas maneras, y se han construido curvas que representan este fenómeno. En términos generales, los problemas en base a la complejidad algorítmica se puede representar a través de las siguientes curvas:

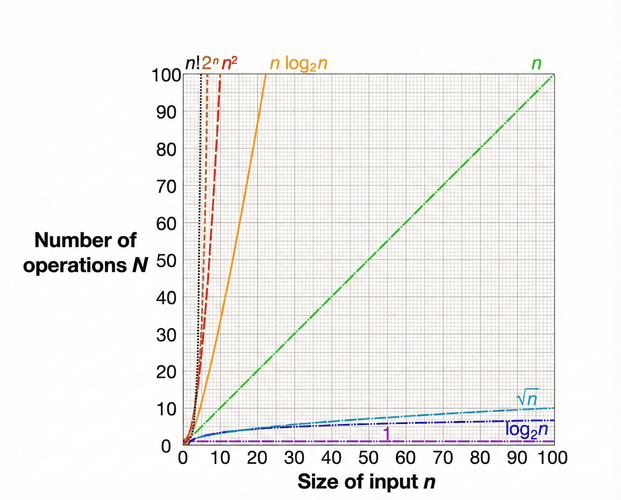
Gemini_Generated_Image_rnssusrnssusrnss (1) (1).png

Donde,

  1. 0(1): Constante. Siempre es lo mismo. Acceder a un transacción en una lista de transacciones.
  2. 0(log n): Logarítmica, creciendo muy lento. Búsqueda binaria de un elemento en una lista.
  3. 0(Raiz cuadrda): Mas lenta que log(n).
  4. 0(n): El tiempo crece proporcionalmente. Recorrer un conjunto de datos una vez.
  5. 0(n log n): Lineal-logarítmica.
  6. 0 (n*n): Cuadrática. Costosa y crece rápido. Si recorro un conjunto de datos, y los comparo entre si, es un ejemplo de n2.
  7. O (2 exponencial de n): Explota rápido, casi inutilizable. Se vuelve muy costosa.
  8. 0 (n!): Factorial. Todas las permutaciones posibles. Si tenemos un conjunto de datos, y queremos saber todas las posibles formas de ordenarlos.

Como se aprecia, a medida que queremos realizar tareas más complejas y trabajar con mayores volúmenes de datos, se vuelve necesario saber cómo optimizar la solución, tanto al momento de guiar como para construir sistemas robustos, no solo en términos de datos, sino también de procesamiento.

Space complexity: Utilizar menos memoria adicional ayuda a aliviar el problema.

El space complexity mide cuánta memoria adicional utiliza un algoritmo para ejecutarse, en función del tamaño de la entrada. Esta memoria incluye variables auxiliares, estructuras temporales (como listas, arrays o matrices) y, en el caso de algoritmos recursivos, la memoria utilizada por la pila de llamadas. No considera la memoria necesaria para almacenar los datos de entrada, sino únicamente la memoria extra que el algoritmo va utilizando durante su ejecución.

Imaginemos nuevamente el ejemplo del profesor. Queremos evaluar si los alumnos se están copiando, junto con asignarles su nota. Si quisiéramos optimizar un poco más la solución, podríamos eliminar parte de la memoria adicional que estamos creando al agregar y procesar los datos, de la siguiente manera:

1def review_tests(d: dict):
2    dup_flags = np.zeros(len(d), dtype=bool)
3

4    # Detect duplicated answers (no auxiliary lists)
5    for i, (_, v1) in enumerate(d.items()):
6        for j, (_, v2) in enumerate(d.items()):
7            if i != j and v1 == v2:
8                dup_flags[i] = True
9                break
10

11    # Grading
12    ground_truth = "I think it's 7"
13    for k in d:
14        d[k] = 5 if d[k] == ground_truth else 0
15

16    return {
17        'array': dup_flags,
18        'note': d
19    }

En este caso, las variables keys y values ya no se almacenan, reduciendo la complejidad del algoritmo de O(3n) a O(n). Esto no significa que deje de ser O(n), ya que la variable dup_flags sigue formando parte de la solución y mantiene un crecimiento lineal.

Conclusión

Estos conceptos suelen quedar fuera de la formación tradicional en ciencia de datos. Sin embargo, entenderlos es clave, ya que muchas soluciones que parecen correctas en entornos pequeños fallan en producción al no considerar fundamentos esenciales de la computación, junto con buenas prácticas de diseño y eficiencia de código.

Ir arriba